译介｜最无趣的数字

原文链接 |  Manon Bischoff | March 3, 2023

你最喜欢的数字是什么？被问到这个问题的时候，很多人会想到一些无理数，像是圆周率（π），自然底数（e），或是 2 的平方根。就算是在自然数中你也能找到一些有内涵的数字，比如 7 个小矮人， 7 宗罪，不吉利的13，以及 42 —— 它随着《银河系搭车指南》而被人熟知。

那大点的数字呢，比如 1,729？ 对大多数人来说，这个数字显然没那么有趣。乍一看，这个数字似乎平平无奇。毕竟它既不是质数，又不是 2 的幂数，也不是平方数。而且每一位数字的的排列也不符合什么明显的规律。这也是数学家 Godfrey Harold Hardy 的想法，他当时刚好搭上了车牌号为 1729 的计程车，去医院看望一位生病的同事 Srinivasa Ramanujan。他将这个"无聊"的数字告诉了这位同事，希望这不是什么不好的兆头。而 Ramanujan 立刻就反驳了他的朋友：「这是个很有趣的数字。它是可以用两对立方数表示的最小的数字。」¹

现在你可能会想，究竟有没有一个完全无趣的数字。这个问题其实是一个悖论：如果真的存在一个数字 $n$ 没有任何有趣的性质，那么这个事实本身就会令它变得非常独特。不过确实存在一个方法能够客观地评价一个数字是否有趣——而且出乎数学家的意料的是，2009 年的一项研究表明，自然数（正整数）明显地被划分到两个阵营：有趣的数字的和无趣的数字。

一本数列百科全书为探索这两种数字分类提供了一个手段。数学家 Neil Sloane 在 1963 年萌生了编纂这样一本百科全书的想法。他当时正在撰写他的博士论文，需要计算一个叫做树形网络图的深度，于是他遇到了这样一串数字：$0, 1, 8, 78, 944, …$。他不懂该如何计算这个数列，所以想知道他的同事们是不是在他们的研究中遇到过类似的数列。但与逻辑或算法不同，当时不存在一个为数列登记在册的途径。所以在十年后，Sloane 发表了他的第一版百科全书：《整数数列大全（A Handbook of Integer Sequence）》。这本书中囊括了 2,400 个被证明在某些特定的计算中很有用的数列。这本书很快就获得了认可。据 Sloane 所说，一位热情的读者如此给出了如此的评价：「我们有《旧约》，我们有《新约》，我们有《整数数列大全》。」

在接下来的几年时间，更多的数列被提交给了 Sloane，一些学术论文中也出现了新的数列。在这些事情的驱动下，这位数学家于 1995 年和他的同事 Simon Plouffe 一同出版了《整数数列百科全书（The Encyclopedia of Integer Sequences）》，收录了大约 5,500 条数列。收录的内容一直在持续增长，好在互联网的出现使得这些数据洪流可以得到控制整理：在 1996 年，《整数数列在线百科全书（the Online Encyclopedia of Integer Sequences, OEIS）》诞生了，它不再对可被收录的数列做任何格式上的限制。到了 2023 年 3 月，它已经收录了 360,000 条记录。任何人都可以提交记录，你要做的就只是说明如何可以生成这条数列，它为何有趣，并且提供它的前几项。在审查员检查过这条记录，确认它满足以上的条件之后，就会公布发表。

除了那些著名的数列之外——比如质数数列 $(2, 3, 5, 7, 11, …)$，2 的幂数数列 $(2, 4, 8, 16, 32, …)$ 或者斐波那契数列 $(1, 1, 2, 3, 5, 8, 13, … )$，OEIS 还收录了一些奇妙的例子，比如用 $n$ 块 $2\times 4$ 的乐高积木来搭建稳定塔结构的方法数量 $(1, 24, 1560, 119580, 10166403, …)$，或者是懒老板数列（lazy caterer’s sequence），$(1, 2, 4, 7, 11, 16, 22, 29,…)$，也就是把披萨切 $n$ 刀能得到的最多块数。

因为有大约 130 人左右对提交的数列进行审查，同时那些常见的数列已经存在了数十年并且在数学爱好者社区中广为人知，这个数列集合基本上可以看作是所有数列集合中比较客观的选择。这使得 OEIS 的数据目录非常适合用来研究数字的受欢迎程度。也就是说，一个数字在列表中出现的次数越多，它就越有趣。

至少 Philippe Guglielmetti 是这么想的。他在维护更新一个法语的博客 Dr. Goulu，在其中一篇博客中，Guglielmetti 再次审视了一位前数学教师曾经表达过的观点：数字 1548 似乎没有任何特殊性质。实际上，这个数字在 OEIS 中出现了 326 次。本文开头出现的 Hardy 对于 1729 的无趣判断其实也是错的：1729 在数据库中出现了 918 次（而且还在剧集《飞出个未来》中频繁出现）。

于是 Guglielmetti 开始调查真正无趣的数字：那些几乎不会出现在，或者完全没有出现在 OEIS 数据中的数字。后者是存在的，比如数字 20067。到三月为止，这是没有出现在任何被收录的数列中的最小的数字，（这也是因为数据库只会存储每个数列的前 180 个字符，否则所有的正整数都会出现在 OEIS 的列表中了）所以 20067 看上去就非常无趣了。相对的，它之后的 20068 则出现在了 6 条记录中。

无趣的数字并没有一个通用的规则，20067 的状态也是可以改变的。也许就在这篇文章被撰写的过程中，一个新的数列被发现，而且它的前 180 个字符中就包含了 20067。不过不管怎么说，OEIS 的记录可以用来衡量数字有趣程度。

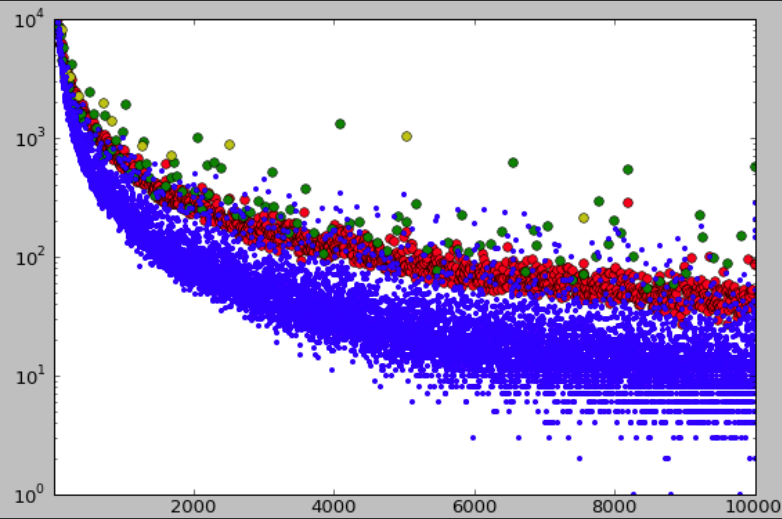
Guglielmetti 继续整理了所有记录中出现的数字，然后把画出了它们的频率。他发现这块点状云呈现出曲线带的形状，频率随着数值的增加而滑落。这并不令人意外，因为只有数列的前几项数字会被存储在 OEIS 中。真正令人意外的是，这条曲线被分成了两条曲线带，其间有一条清晰可见的空隙。也就是说，OEIS 数据库中的数字要么就极其常见，要么就非常稀有。

被这个结果吸引的 Guglielmetti 咨询了数学家 Jean-Paul Delahaye。他常常为 Pour la Science —— Scientific American 的法语姐妹刊物 —— 撰写科普文章。Guglielmetti 想知道数学家们是否已经研究过这种现象：答案是否定的。于是 Delahaye 和他的同事，Nicolas Gauvrit 与 Hector Zenil，接下了这个课题，做了更加深入的调查研究。他们使用了算法信息理论的结果，这种方法通过算法来表达一个描述，然后用最短的算法长度来衡量这个描述的复杂度。举例来说，类似于 47934 这种五个随机数位组成的数字（算法描述为「由数字 4、7、9、3、4 组成的序列」）就要比数字16384 （算法描述为「$2^{14}$」）更难描述。根据算法信息理论，有更多性质的数字通常会有更低的复杂度。也就是说，在 OEIS 中频繁出现的数字应该更容易去描述。² Delahaye，Gauvrit 和 Zenil 的工作显示，通过信息理论可以给出与 Guglielmetti 的曲线类似的自然数的复杂度轨迹。但是这并不能解释那条以 Neil Sloane 命名的「Sloane 空隙」。

三位数学家认为这条空隙可能是社会学因素导致的，比如对某些特定数字的倾向性。为了证明这点，他们运行了一个被称为蒙特卡罗方法的模拟：他们设计了一个函数，这个函数是一个自然数到自然数的映射——映射的结果中小数值会比大数值更容易出现。他们把一些随机数输入函数，然后绘制出输出结果的频率。通过这个实验研究者们得到了一个粗略的滑坡曲线，与 OEIS 数据的曲线类似，但和信息理论的分析一样，没有空隙。

为了更好的理解那条空隙是如何出现的，你必须观察哪些数字落入了哪条曲线带。Sloane 空隙对于 300 以内的小数值并不明显，只有对较大的数字才清晰起来：在 300 到 10,000 的数字中，有 18% 的的数字在「有趣带」中，剩下的 82% 则属于「无趣」的数值。这些有趣的数字包括了所有数字中 95.2% 的平方数，99.7% 的质数，以及 39% 的多质因子合数（numbers with many prime factors）。单是这三种类型的数字就足以占据接近 88% 的有趣数字了。而剩下的有趣数字则有更加显著的性质，比如 1111 或者 $2^n+1$ 和 $2^n-1$。

根据信息理论，那些非常有趣的数字应该有很低的复杂度，这意味着它们应该非常容易被描述。但是如果数学家们对相同复杂度的数值有不同的偏好，就可能会出现 Sloane 空隙，正如 Delahaye，Gauvrit 和 Zenil 所说。比如说，从信息理论的角度来看，$2^n+1$ 和 $2^n+2$ 有相同的复杂度，但是只有前者落在了「有趣带」中。这是因为这些数字可以考察到一些质数，所以它们出现在了更多的数列中。

因此「有趣」和「无趣」的分歧似乎是由我们的判断导致的，比如我们为质数赋予了更多的重要性。所以当你被问到你最喜欢的数字时，如果你想给出一个比较有新意的答案，你可以给出一个类似 20,067 这种还没有出现在任何 Sloane 的百科全书记录中的数字。